When developing models that intend to model the dynamics of a business, such as in business science models, there are many potential ways of modeling certain specific dynamics. Such as should the price response be linear, or nonlinear, where there are basically an infinite amount of possible functions that could apply.
High-level domain knowledge
We think the correct thing is to express high-level dynamics that come from knowledge of the specific business, which ensures sane causality.
For this example, we will do a small model that consists of online media (Online), offline media (Offline), brand awareness (Brand), net promoter score (NPS), product price (Price) and number of items sold (Sales).
Just from pure causality we know that the business buys advertisements in online and offline media and that drives Brand, NPS, and Sales. So by knowing this we can eliminate relationships such as illustrated in the figure on the right.
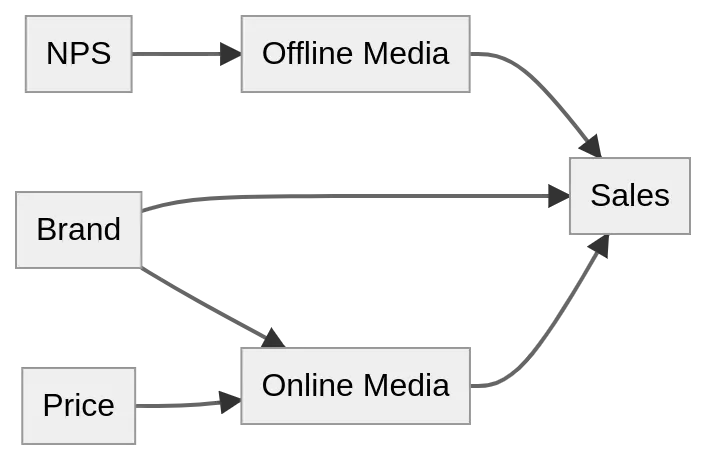
Since we know this does not adhere to the correct causality of the real world. What one instead wants to do is to have a conversation with a person that actually understands the dynamics of the specific business to construct what is considered to be the correct causal relationship.
In this case, we assume that Brand and NPS are unrelated to each other since the brand measures a high-level awareness in the population and NPS is direct customer interaction. There is a possibility of NPS affecting the brand, but we will ignore that for the sake of this example. So for this case, we assume a causal relationship that looks like the right hand figure.
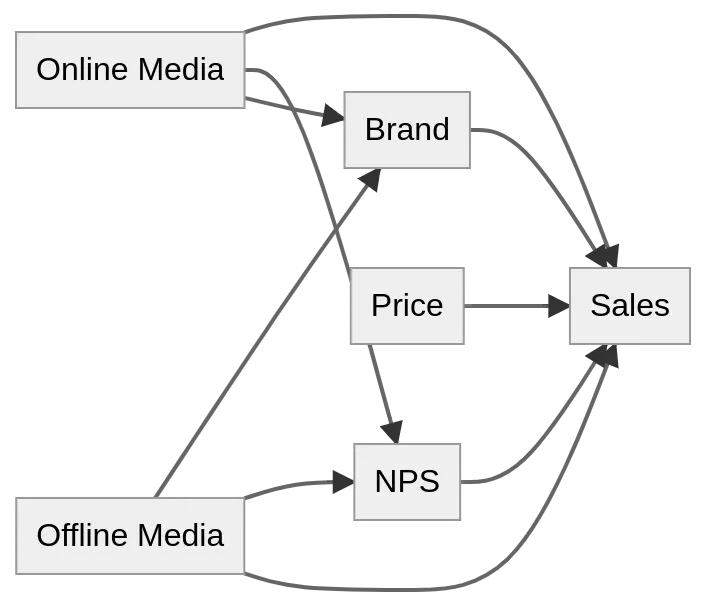
This is a simplified version for illustrative purposes, in reality, there are most likely more factors and relationships that will come into play in a production model such as macro economical factors, seasonality, etc.
What one also should be able to encode on this high level is if there are any strict relationships such as when Brand goes up Sales needs to go up i.e. if more people know about the business and like the business sales should not be negatively impacted by this.
Low-level domain knowledge
For high-level domain knowledge, one thinks about the causal relationship between the different variables. With low-level domain knowledge, one focuses on how to model the specific ways to model a variable such as offline media, and how to model the interaction between variables such as how Offline Media and price interact to impact sales.
Variable specific formulations
Depending on what the input data is, such as online media, offline media, price, NPS, etc. they all need to be thought about carefully of how their dynamics behave and how to best capture them.
Let’s take price as an example, one can assume that if the price goes up 10 % it will have a negative impact on sales, while if the price goes down 10 % it will have a positive effect on sales. Price might also have some non linear dynamics, such as a 30 % drop in price is 10x more impactful than a 10 % drop in price.
So one needs a mathematical formulation that captures this behavior in a sane manner. This could be achieved by to model it as the inverse of price, i.e., 1/Price. But it could also be modeled linearly by multiplying the price with -1, such a larger value would have a bigger negative effect. By model it linearly one adheres to the correct relationship of: if price goes up, sales goes down, if price goes down sales go up.
But one does not capture any non linear dynamics of an aggressive sale. But maybe an aggressive sale has never occurred as of yet, and a linear price response is additive in this specific case. As one thinks about these local dynamics one quickly realizes there might be exponentially many possible ways of modeling the dynamics of price and the other variables as well. So what one actually wants to do is to find a few ways of modeling dynamics with the right amount of flexibility and try all of them.
Interactions
How different variables interact with each other can happen in various ways. They can both contribute directly to the new variable or the could to turn the variable on and off, i.e., in the basic case one could model sales linearly like
\[ Sales=Price+NPS+Brand+Online+Offline \]
With some coefficients in front of each variable. But maybe it needs some more complex dynamics with multiplicative effects
\[Sales=Brand·NPS·(Price+Online+Offline) \]
Such as if the brand awareness is 0 one can not sell anything and if the customers are unhappy one can not sell anything.
Also here one quickly realizes relying on a single model structure is foolish. So also here we need to actually try several different ways of doing it. That is why incorporating some high-level domain knowledge such as “NPS needs to have a positive effect on sales”, can help limit the potential combinations.
Combining specific formulations and interactions
In our example above, Offline Media contributes to both Brand, NPS and Sales. But how offline media impacts and interacts with them may be different, so that is why one needs to try different combinations for each interaction. Below this is illustrated by having two types of modeling media and how that could impact Brand, NPS and Sales.
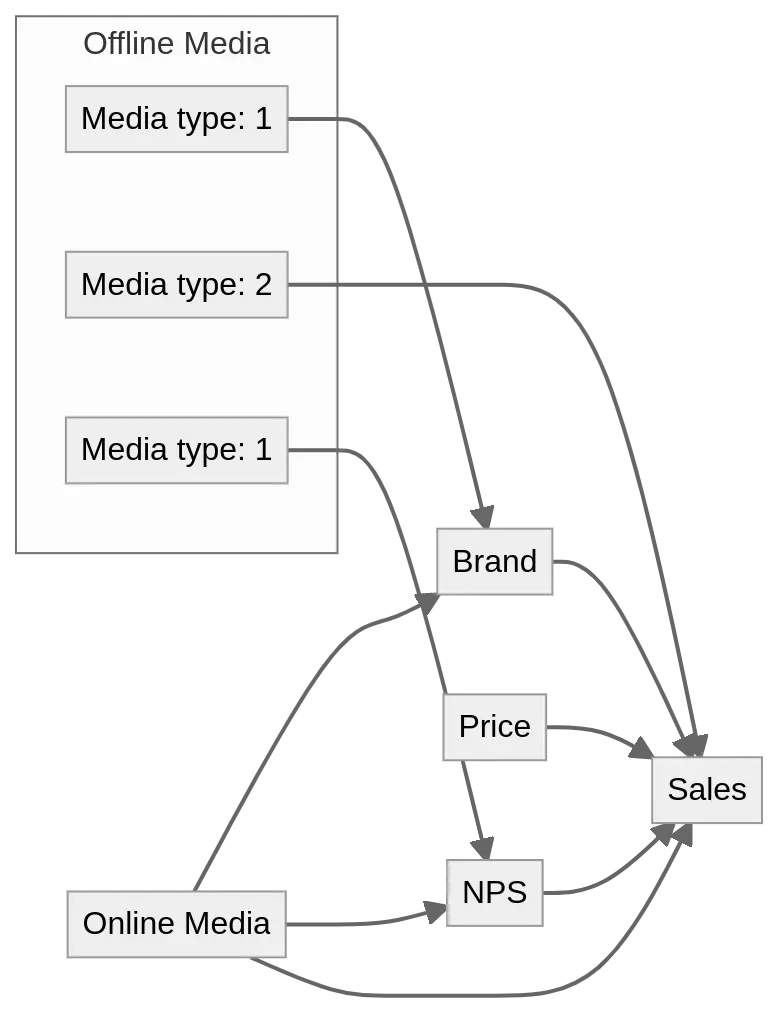
The same setup holds true for Online Media, Price etc. Without actually trying what combinations it is very hard to tell which combination will prove to be the most successful. This comes back to the quote
“All models are wrong, but some are useful” - George E. P. Box
Where we know that the model will not be perfect, but by trying different combinations of how things are designed, one can hope to find a model that is actually useful. Rather than having a single model structure and force it to adhere to high-level domain knowledge while compromising low-level domain knowledge.
Model combinations at scale
As the amount of possible ways of modeling each variable grows one quickly get hundreds to thousands of possible combinations, so in order to actually be able to try all of the combinations and still have the correct uncertainty estimation from Bayesian Inference we rely on a technique called Variational Inference.
Variational inference turns the normal sampling problem of Bayesian inference into an optimization problem that is a lot faster to solve. So instead of a model taking hours to train it takes minutes to train. Combining this with elastic compute resources, one can fit the models in parallel further reducing the time to actually try all the combinations.